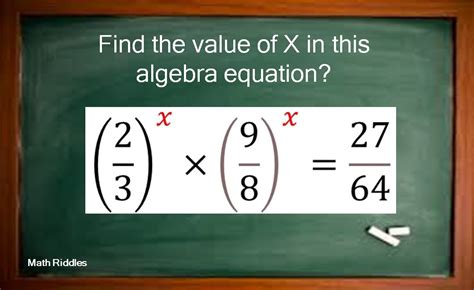Introduction
Determining the value of an unknown variable (x) is a fundamental mathematical skill used in various fields, from algebra to calculus. This guide provides a comprehensive walkthrough of different methods to find the value of x in equations.

Step-by-Step Approach
1. Isolate the Variable
- Step 1: Identify the equation containing the unknown variable x.
- Step 2: Perform operations such as adding, subtracting, multiplying, or dividing by the same constant on both sides of the equation to isolate x on one side.
2. Simplify the Equation
- Step 3: Simplify the equation by combining like terms and removing any unnecessary constants or variables.
- Step 4: Bring all terms containing x to one side and the remaining constants to the other side.
3. Solve for x
- Step 5: Determine the appropriate mathematical operation to solve for x based on the equation’s form. This may involve dividing, taking the square root, or using other algebraic techniques.
- Step 6: Perform the operation to find the value of x.
Linear Equations (x = a + b)
Linear equations are first-degree equations of the form ax + b = c, where a, b, and c are constants and a ≠ 0.
- To find the value of x:
- Subtract b from both sides: ax = c – b
- Divide both sides by a: x = (c – b)/a
Quadratic Equations (x^2 + bx + c = 0)
Quadratic equations are second-degree equations of the form ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0.
- To find the value of x using the quadratic formula:
- x = (-b ± sqrt(b^2 – 4ac))/(2a)
Exponential Equations (y = a^x)
Exponential equations are equations where the variable x appears as an exponent.
- To find the value of x using logarithms:
- log(y) = x * log(a)
- x = log(y)/log(a)
Logarithmic Equations (log(x) = a)
Logarithmic equations are equations where the variable x appears as the argument of a logarithm.
- To find the value of x using exponential equations:
- 10^a = x
- e^a = x
Applications and Use Cases in Industry
Finding the value of x has applications in numerous fields, including:
- Engineering: Designing and analyzing structures, fluid dynamics, and material properties.
- Finance: Calculating interest rates, loan payments, and investment returns.
- Physics: Determining velocity, acceleration, and force from experimental data.
- Data Science: Analyzing trends, predicting outcomes, and optimizing algorithms.
Innovative Ideas for New Applications
By leveraging the mathematical concept of finding the value of x, we can unlock opportunities for novel applications in emerging fields:
- Bioinformatics: Modeling genetic sequences, analyzing gene expression patterns, and identifying disease biomarkers.
- Artificial Intelligence: Solving complex optimization problems, training neural networks, and developing self-driving systems.
- Materials Science: Designing new materials with tailored properties, optimizing production processes, and predicting material behavior.
Market Insights and Trends
- According to the National Science Foundation, the demand for professionals with strong mathematical skills is projected to increase significantly by 2025.
- The global market for mathematical software is expected to reach $18.5 billion by 2025, driven by the growing adoption of data analytics and machine learning.
- A survey by the Mathematical Association of America found that over 80% of respondents believe mathematics is essential for success in the 21st-century workforce.
Conclusion
Finding the value of x is a fundamental mathematical skill with far-reaching applications across various industries. By understanding the step-by-step approach and utilizing different methods based on the equation’s form, we can effectively determine the value of x. As we continue to explore new applications and leverage mathematical tools, the ability to find the value of x will play a crucial role in shaping the advancements of the future.
Frequently Asked Questions (FAQs)
- Q: How do I know which method to use to find the value of x?
-
A: The appropriate method depends on the form of the equation. Linear equations require simple algebraic operations, while quadratic equations use the quadratic formula and exponential equations involve logarithms.
-
Q: What happens if the equation is not in a standard form?
-
A: It may be necessary to manipulate the equation to bring it into a recognizable form before using the appropriate method.
-
Q: How can I check if my answer is correct?
- A: Substitute the calculated value of x back into the original equation and verify if it satisfies the equation.